Steiner Triple Systems
How to Create a Steiner Triple System from a Latin Square
Introduction
A Steiner Triple System (STS) is a Set of Sets. Each subset contains exactly three elements and each pair of elements appears in exactly one subset (Weisstein). To denote the values in a Steiner Triple System, we give the largest value in the set, this is called the order. We call $STS(v)$ a Steiner Triple System of order $v$.
To make this definition more clear, we can look at an example. Here is one $STS(7)$ from (Weisstein).
\[STS(7)=\lbrace \lbrace 1,2,4\rbrace , \lbrace 2,3,5\rbrace , \lbrace 3,4,6\rbrace , \lbrace 4,5,7\rbrace , \lbrace 5,6,1\rbrace , \lbrace 6,7,2\rbrace , \lbrace 7,1,3\rbrace \rbrace\]Remember that a set is a unordered collection with no duplicates. That means that $\lbrace 1,2,4\rbrace$ and $\lbrace 2,4,1\rbrace$ are the same set. The first triple contains the following pairs $\lbrace 1,2\rbrace $, $\lbrace 1,4\rbrace$, and $\lbrace 2,4\rbrace$. Notice that these pairs do not appear in any other triples. This system is small enough we can show all pairs appear exactly once exhaustively. This is a useful example to prepare you for the later sections.
We label each triple to make it easier to talk about them. This will also make it more obvious each pair appears in exactly one triple.
| Name | Triple |
|---|---|
| $t_{0}$ | $\lbrace 1,2,4\rbrace$ |
| $t_{1}$ | $\lbrace 2,3,5\rbrace$ |
| $t_{2}$ | $\lbrace 3,4,6\rbrace$ |
| $t_{3}$ | $\lbrace 4,5,7\rbrace$ |
| $t_{4}$ | $\lbrace 5,6,1\rbrace$ |
| $t_{5}$ | $\lbrace 6,7,2\rbrace$ |
| $t_{6}$ | $\lbrace 7,1,3\rbrace$ |
Next, we list every pair of two numbers between $1$ and $7$. We match each pair to the triple it appears in. Remember, each pair must appear exactly one time.
| Pair | Triple It Appears In |
|---|---|
| $\lbrace 1,2\rbrace$ | $t_{0}=\lbrace 1,2,4\rbrace$ |
| $\lbrace 1,3\rbrace$ | $t_{6}=\lbrace 7,1,3\rbrace$ |
| $\lbrace 1,4\rbrace$ | $t_{0}=\lbrace 1,2,4\rbrace$ |
| $\lbrace 1,5\rbrace$ | $t_{4}=\lbrace 5,6,1\rbrace$ |
| $\lbrace 1,6\rbrace$ | $t_{4}=\lbrace 5,6,1\rbrace$ |
| $\lbrace 1,7\rbrace$ | $t_{6}=\lbrace 7,1,3\rbrace$ |
| $\lbrace 2,3\rbrace$ | $t_{1}=\lbrace 2,3,5\rbrace$ |
| $\lbrace 2,4\rbrace$ | $t_{0}=\lbrace 1,2,4\rbrace$ |
| $\lbrace 2,5\rbrace$ | $t_{1}=\lbrace 2,3,5\rbrace$ |
| $\lbrace 2,6\rbrace$ | $t_{5}=\lbrace 6,7,2\rbrace$ |
| $\lbrace 2,7\rbrace$ | $t_{5}=\lbrace 6,7,2\rbrace$ |
| $\lbrace 3,4\rbrace$ | $t_{2}=\lbrace 3,4,6\rbrace$ |
| $\lbrace 3,5\rbrace$ | $t_{1}=\lbrace 2,3,5\rbrace$ |
| $\lbrace 3,6\rbrace$ | $t_{2}=\lbrace 3,4,6\rbrace$ |
| $\lbrace 3,7\rbrace$ | $t_{6}=\lbrace 7,1,3\rbrace$ |
| $\lbrace 4,5\rbrace$ | $t_{3}=\lbrace 4,5,7\rbrace$ |
| $\lbrace 4,6\rbrace$ | $t_{2}=\lbrace 3,4,6\rbrace$ |
| $\lbrace 4,7\rbrace$ | $t_{3}=\lbrace 4,5,7\rbrace$ |
| $\lbrace 5,6\rbrace$ | $t_{4}=\lbrace 5,6,1\rbrace$ |
| $\lbrace 5,7\rbrace$ | $t_{3}=\lbrace 4,5,7\rbrace$ |
| $\lbrace 6,7\rbrace$ | $t_{5}=\lbrace 6,7,2\rbrace$ |
This is actually the only nonisomorphic Steiner Triple Systems of order 7 (Colbourn 1999). There are many isomorphic Steiner Triple Systems of order $7$. For example, we could swap $5$ and $7$ in every triple they appear and we could create a new $STS(7)$.
A more general way to describe our system would be using a list of values.
\[X=[1,2,3,4,5,6,7]\]Then $STS(7)$ is given as
\[\begin{align*} STS(7)=&\lbrace \lbrace X_0,X_1,X_3\rbrace , \lbrace X_1,X_2,X_4\rbrace , \lbrace X_2,X_3,X_5\rbrace , \\ &\lbrace X_3,X_4,X_6\rbrace , \lbrace X_4,X_5,X_0\rbrace , \lbrace X_5,X_6,X_1\rbrace , \lbrace X_6,X_0,X_2\rbrace \rbrace \end{align*}\]We could generate another valid (but isomorphic) $STS(7)$ by changing the order of the elements in $X$.
Let $X=[7,1,6,2,5,3,4]$ and you can create another $STS(7)$. This is isomorphic to the original. You are just changing the label of each element. If we describe $X$ as a set, then this order doesn’t matter and we are just talking about $STS$ that are nonisomporhic.
We are now prepared to give a more formal description.
$STS(v)$ is a Steiner Triple System of order $v$ is a 2-tuple containing two sets, $X$ and $B$. $X$ is a set of elements where $\lvert X \rvert = v$ and $v \ge 3$. $B$ is a set of triples selected from $X$ such that every pair in $X$ appears exactly once in a triple of $B$. Since the values of $X$ are obvious from $B$, it doesn’t need to be explicitly written very often.
There only exist $STS(v)$ if $v \mod 6 \equiv 1$ or $v \mod 6 \equiv 3$ (Weisstein). Triple systems can be further generalized by allowing the pairs to appear more times, for example allowing each pair to appear twice (Colbourn 1999).
Latin Squares
To create Steiner Triple Systems, we will use Latin Squares. A Latin Square is an $n$ by $n$ array such that each element appears exactly once in each column and each row. Given a partial Latin Square completing the missing values is an NP-Complete Problem (Colbourn 1984). For the remainder of this article, we will just assume that any Latin Squares we need appears by magic.
Let’s say we want a Latin Square with elements $1$, $2$, and $3$. We have $n=3$ elements. That means we need a $3$ by $3$ array. Each of the three elements must appear exactly one time in each row and in each column.
\[L_{3}=\begin{bmatrix} 1 & 2 & 3 \\ 2 & 3 & 1 \\ 3 & 1 & 2 \end{bmatrix}\]Latin Squares were studied as far back as the 1700s by Choi Seok-Jeong and later by Leonhard Euler (Colbourn 1984).
Steiner Triple System of Order 3
There is only one answer for $STS(3)$. We only have three elements $X=\lbrace 1,2,3\rbrace $. We can only make one triple that contains all three elements.
$STS(3)=\lbrace \lbrace 1,2,3\rbrace \rbrace $
This is the smallest non-empty solution to $STS(v)$. It fits into the pattern $v \mod 6 \equiv 3$. We could also give $v=1$ since $v \mod 6 \equiv 1$ is also allowed. This is a trivially empty set $STS(1)=\lbrace \rbrace $. We cannot make any triples without three elements.
Steiner Triple Systems get interesting starting with order $7$. We will actually jump ahead and look at order $9$ first. We will see that its construction is a little easier since $9 \mod 3 = 0$.
Steiner Triple System of Order 9
We know that $STS(v)$ only exists if $v \mod 6 \equiv 1$ or $v \mod 6 \equiv 3$. We can break this up into two groups. Each will have a slightly different construction. Let $n \ge 0$ and $v= 6n+3$. By definition this construction will give us values where $v \mod 6 \equiv 3$.
The first few values of $n$ and $v$ are given below. We already handled $v=3$, which corresponds to $n=0$. In this section, we will construct $STS(9)$ using $n=1$.
| $n$ | $v$ |
|---|---|
| $0$ | $3$ |
| $1$ | $9$ |
| $2$ | $15$ |
| $3$ | $21$ |
First, you need a Latin Square with values $L=\lbrace 0,1,\cdots,2n\rbrace $. We define this as a function $i \circ j$ where $i$ is the row and $j$ is the column (Moura, Slide 9). We start with a Latin Square containing $0$, $1$, and $2$.
\[L_{3}=\begin{bmatrix} 0 & 2 & 1 \\ 2 & 1 & 0 \\ 1 & 0 & 2 \end{bmatrix}\]We then use it as a table for the function $i \circ j$.
| circ(i,j) | j=0 | j=1 | j=2 |
|---|---|---|---|
| i=0 | 0 | 2 | 1 |
| i=1 | 2 | 1 | 0 |
| i=2 | 1 | 0 | 2 |
This function must be idempotent and commutative (Colbourn 1999). Idempotent means that $i \circ i = i$ and commutative means $i \circ j = j \circ i$ (Moura, Slide 9). Construction of the Latin Square needs to meet these properties. That is a whole problem itself. We will again just say that magic created the right Latin Square. You might want to check the example Latin Square from the earlier section and see if it meets these requirements.
We have our function. We also need the numbers to select to put in the $STS(9)$. We create a $\frac{v}{3}$ by $3$ array containing the values. Remember that since $v \mod 6 = 3$ we know that $\frac{v}{3}$ is a whole number.
The set of values we are putting in the triples is $X$.
\[X=\lbrace 1,2,3,4,5,6,7,8,9\rbrace\]We call the $\frac{v}{3}$ by $3$ array $M$.
\[M = \begin{bmatrix} 1 & 4 & 7 \\ 2 & 5 & 8 \\ 3 & 6 & 9 \\ \end{bmatrix}\]The general construction of $M$ given $n$ is
\[M_{n} = \begin{bmatrix} 1 & v/3+1 & 2v/3+1 \\ 2 & v/3+2 & 2v/3+2\\ \vdots & \vdots & \vdots \\ v/3 & 2v/3 & v \\ \end{bmatrix}\]We can now generate a $STS(9)$. The algorithm is described below (Moura, Slide 12). This is called a Bose construction method.
def bose(n,M,circ):
STS=makeSet()
for x in range(0,2*n+1):
S=makeSet(M[x][0],M[x][1],M[x][2])
STS = union(STS,makeSet(S))
for y in range(0,2*n+1):
for x in range(0,y):
t1=makeSet(M[x][0],M[y][0],M[circ(x,y)][1])
t2=makeSet(M[x][1],M[y][1],M[circ(x,y)][2])
t3=makeSet(M[x][2],M[y][2],M[circ(x,y)][0])
newTriples=makeSet(t1,t2,t3)
STS=union(STS,newTriples)
return STS
Running this function with the $i \circ j$ and $M$ values given above will return the following system.
\[\lbrace \lbrace 1, 4, 7\rbrace , \lbrace 2, 5, 8\rbrace , \lbrace 3, 6, 9\rbrace , \lbrace 1, 2, 6\rbrace , \lbrace 4, 5, 9\rbrace , \lbrace 7, 8, 3\rbrace , \\ \lbrace 1, 3, 5\rbrace , \lbrace 4, 6, 8\rbrace , \lbrace 7, 9, 2\rbrace , \lbrace 2, 3, 4\rbrace , \lbrace 5, 6, 7\rbrace , \lbrace 8, 9, 1\rbrace \rbrace\]You can check that this is a valid solution to $STS(9)$. It is not the solution given in (Weisstein). This solution is isomorphic to that one. We just need to change the value of $M$.
\[M=\begin{bmatrix} 1 & 4 & 7 \\ 2 & 5 & 8 \\ 9 & 3 & 6 \end{bmatrix}\]This will give us the set from (Weisstein).
\[\lbrace \lbrace 1, 4, 7\rbrace , \lbrace 2, 5, 8\rbrace , \lbrace 9, 3, 6\rbrace , \lbrace 1, 2, 3\rbrace , \lbrace 4, 5, 6\rbrace , \lbrace 7, 8, 9\rbrace , \\ \lbrace 1, 9, 5\rbrace , \lbrace 4, 3, 8\rbrace , \lbrace 7, 6, 2\rbrace , \lbrace 2, 9, 4\rbrace , \lbrace 5, 3, 7\rbrace , \lbrace 8, 6, 1\rbrace \rbrace\]We can generate any isomorphic $STS(9)$ related to our Latin Square by just changing the values in $M$. As long as it is an $\frac{v}{3}$ by 3 array containing values $(1,2,\cdots,v)$ we will get a valid solution. This is the only nonisomorphic solution to $STS(9)$, every solution is just a different ordering of $M$ (Colbourn 1999).
Steiner Triple System of Order 7
The reason we skipped to $STS(9)$ first is because $9/3=3$. With $STS(7)$, this division has a remainder. If we want to divide $7$ numbers into $3$ columns, there will be one value left over. This value makes the algorithm a little more complex.
We are now in the situation where $v \mod 6 \equiv 1$. We can again introduce an $n$ and define $v= 6n+1$. Some values we can get this time are shown in the below table. Remember that $STS(1)$ is trivially empty since there are not enough elements.
| $n$ | $v$ |
|---|---|
| 0 | 1 |
| 1 | 7 |
| 2 | 13 |
| 3 | 19 |
This time, we make our $i \circ j$ operator from a half-idempotent Latin Square of size $2n$ by $2n$. A half-idempotent Latin Square means $i \circ i = (n+i) \circ (n+i)$ for all $0 \le i \le n-1$. An example Latin Square from (Moura, Slide 16) is given below. This is the Latin Square for $n=2$ since the property is a little more obvious with a larger Latin Square.
\[L_{4}=\begin{bmatrix} 0 & 1 & 2 & 3 \\ 1 & 2 & 3 & 0 \\ 2 & 3 & 0 & 1 \\ 3 & 0 & 1 & 2 \\ \end{bmatrix}\]We are just using $n=1$ which means we need a Latin Square of size $2$ by $2$.
\[L_{2}=\begin{bmatrix} 0 & 1 \\ 1 & 0 \\ \end{bmatrix}\]We have a new version of $i \circ j$ based on this Latin Square.
Next, we need a new $M$. We can account for all but one of the elements in $STS(7)$.
\[M=\begin{bmatrix} 1 & 3 & 5 \\ 2 & 4 & 6 \end{bmatrix}\]We have one element, $7$, missing. This is traditionally called the $\infty$ element, which is super cool sounding (Colbourn 1999; Moura, Slide 17).
\[\infty=7\]We can now generate a $STS(7)$. The algorithm is described below (Moura, Slide 17). This is called a Skolem construction method.
def skolem(n,M,inf,circ):
STS=makeSet()
for x in range(0,n):
t1=makeSet(M[x][0], M[x][1], M[x][2])
t2=makeSet(inf, M[n+x][0], M[x][1])
t3=makeSet(inf, M[n+x][1], M[x][2])
t4=makeSet(inf, M[n+x][2], M[x][0])
newTriples=makeSet(t1,t2,t3,t4)
STS=union(STS,newTriples)
for y in range(0,2*n):
for x in range(0,y):
t1=makeSet(M[x][0], M[y][0], M[circ(x,y)][1])
t2=makeSet(M[x][1], M[y][1], M[circ(x,y)][2])
t3=makeSet(M[x][2], M[y][2], M[circ(x,y)][0])
newTriples=makeSet(t1,t2,t3)
STS=union(STS,newTriples)
return STS
Running this on the values we have already established returns a solution to $STS(7)$.
\[\lbrace \lbrace 1, 3, 5\rbrace , \lbrace 7, 2, 3\rbrace , \lbrace 7, 4, 5\rbrace , \lbrace 7, 6, 1\rbrace , \lbrace 1, 2, 4\rbrace , \lbrace 3, 4, 6\rbrace , \lbrace 5, 6, 2\rbrace \rbrace\]This is again a different but isomorphic solution compared to the one presented in (Weisstein). We can get that solution by changing $M$.
\[M=\begin{bmatrix} 2 & 3 & 5 \\ 1 & 4 & 6 \end{bmatrix}\]The construction now gives us the solution from (Weisstein).
\[\lbrace \lbrace 2, 3, 5\rbrace , \lbrace 7, 1, 3\rbrace , \lbrace 7, 4, 5\rbrace , \lbrace 7, 6, 2\rbrace , \lbrace 2, 1, 4\rbrace , \lbrace 3, 4, 6\rbrace , \lbrace 5, 6, 1\rbrace \rbrace\]We can generate any isomorphic $STS(7)$ related to our Latin Square by just changing the values in $M$. This is the only nonisomorphic solution to $STS(7)$, every solution is just a different ordering of $M$ (Colbourn 1999).
Conclusion
We have defined what a Steiner Triple System is. The collection $STS(v)$ is a set of sets. The subsets are triples and made of elements selected from $X=\lbrace 1,2,\cdots, v\rbrace $. Each pair of elements in $X$ appears in exactly one triple. We must have enough triples to allow each pair to appear exactly once.
For a given $v$, there are many isomorphic solutions to $STS(v)$. These are just relabeling the same solution. For the systems we examined, there was one 1 nonisomorphic solution. This will no longer remain true as $v$ increases. The constructions we have shown work for $v \mod 6 \equiv 1$ and $v \mod 6 \equiv 3$. There are the only values of $v$ that STS exist for, so we have covered all possible answers (Weisstein).
The algorithms given to construct $STS(v)$ are depended on Latin Squares with certain properties. Finding the correct Latin Square is a whole problem in itself. Colbourn shows that completing a partial Latin Square is NP-Complete (1984). If we somehow manage to find a Latin Square, we can then generate the related Steiner Triple System. We can actually generate all isomorphic systems from the Latin Square.
We can wrap everything up into one nice big algorithm.
def STS(v):
n=v//6
#v has a remainder of 1 use Skolem
if v%6==1:
M=makeM(v)
inf = getInf(v)
circ = getLS(v)
return skolem(n,M,inf,circ)
#v has a remainder of 3, use Bose
if v%6==3:
M = makeM(v)
circ = getLS(v)
return bose(n,M,circ)
#No Solutions
return makeSet()
Triple Systems can be generalized in many ways (Colbourn 1999). They appear in many areas of Combinatorics. There are also relationed to graph theory problems.
The solution to $STS(v)$ is equivalent to taking a complete graph of $K_{v}$ points and partitioning it into triangles (Moura, Slide 5). The triangles for one of our solutions to $STS(7)$ is shown below.
These triangles are based on
\[\begin{align*} STS(7)=& \lbrace \lbrace 1, 3, 5\rbrace , \lbrace 7, 2, 3\rbrace , \lbrace 7, 4, 5\rbrace , \lbrace 7, 6, 1\rbrace , \lbrace 1, 2, 4\rbrace , \lbrace 3, 4, 6\rbrace , \lbrace 5, 6, 2\rbrace \rbrace \end{align*}\]Each triple denotes one triangle.
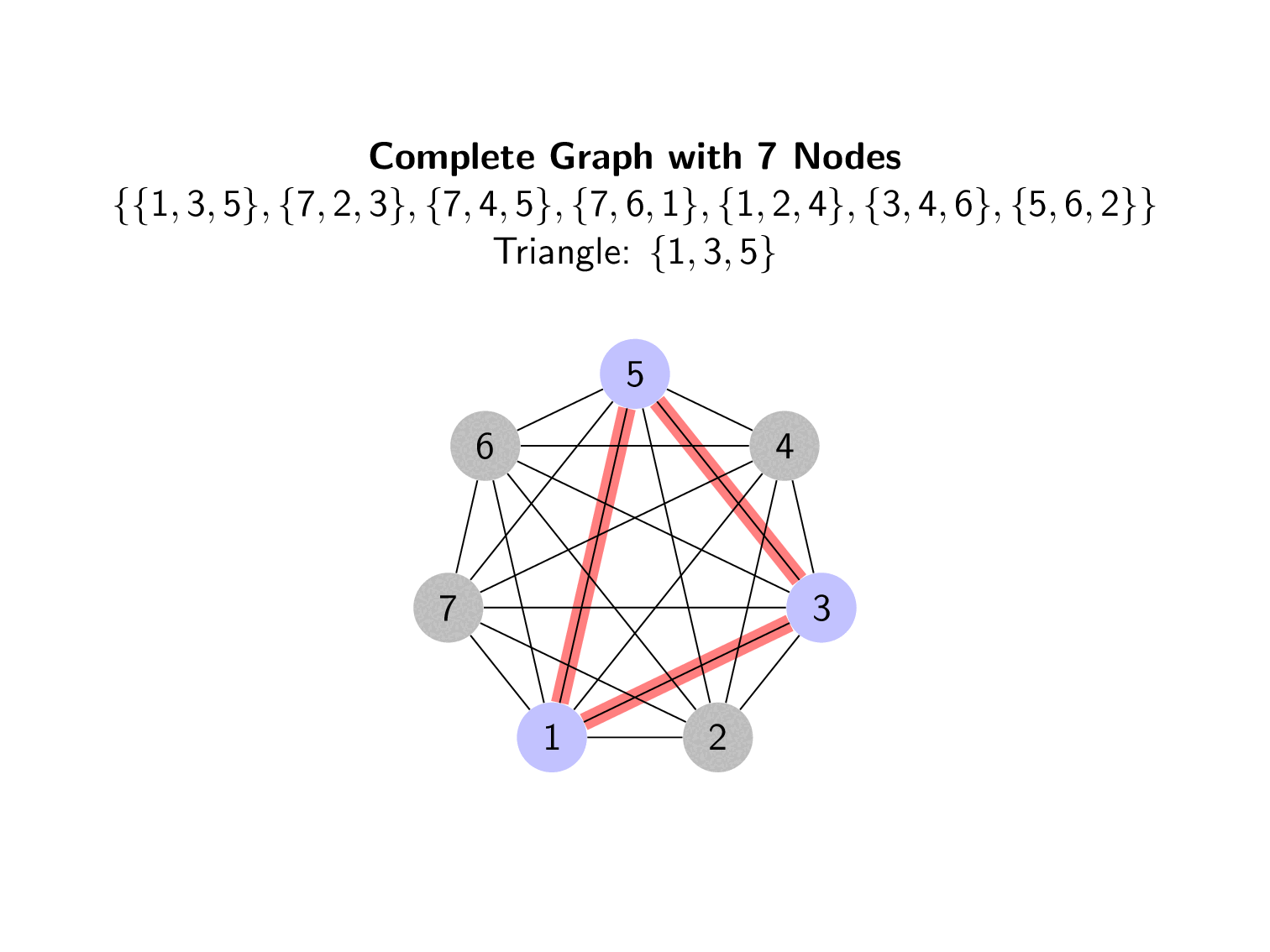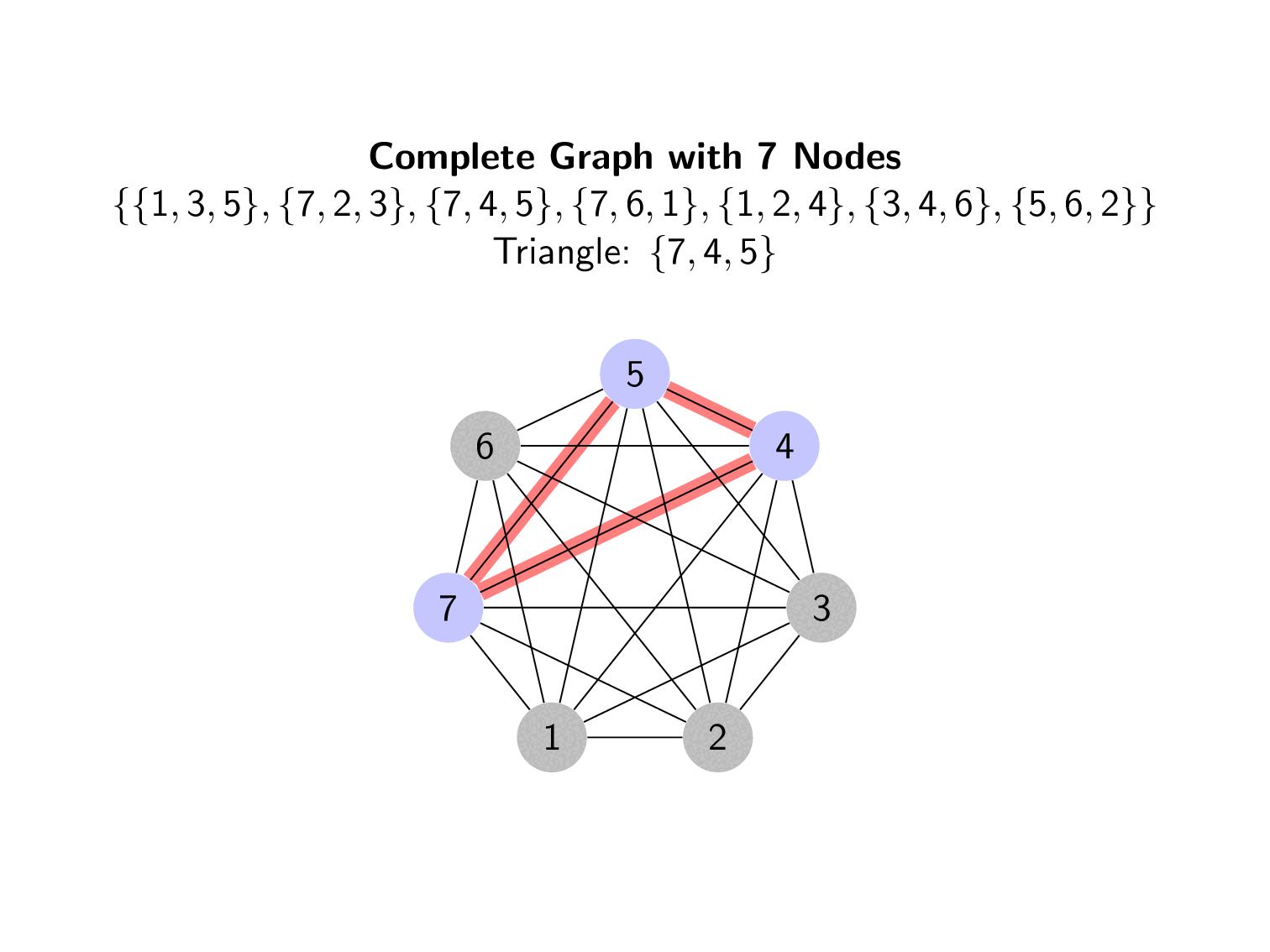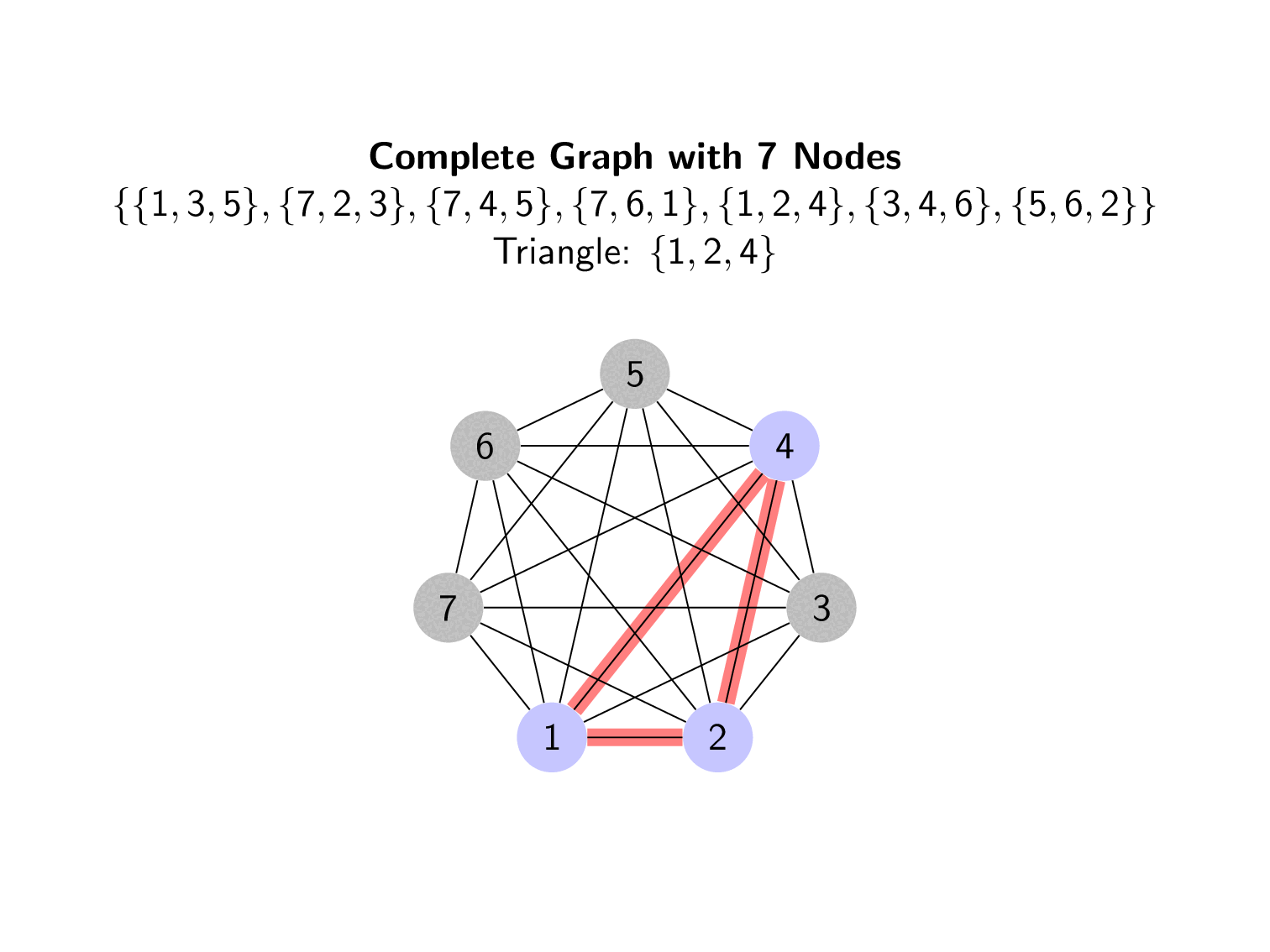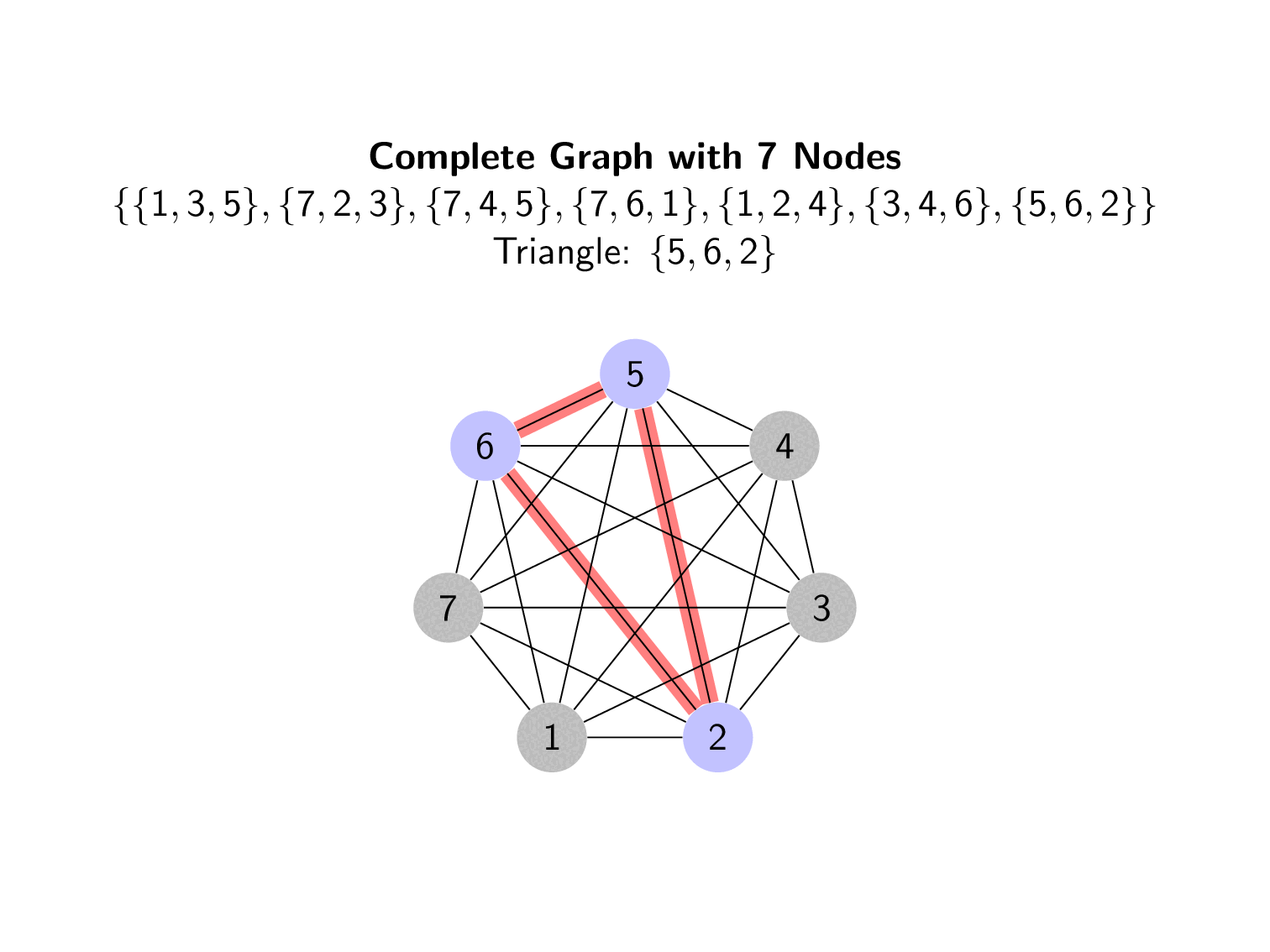
There are many areas of investigation related to Steiner Triple Systems and other related Triple Systems. Often related to counting how many nonisomorphic systems exist or determining algorithms to create systems of specific orders. Both the algorithms shown here are hindered by the need for a Latin Square with specific properties.
Steiner Triple Systems are interesting numerical systems and should be of interest to Mathematicians, Computer Scientists, and anyone who enjoys mathematical puzzles.
References
Colbourn, Charles J. “The Complexity of Completing Partial Latin Squares.” Discrete Applied Mathematics, vol. 8, no. 1, 1984, pp. 25-30., https://doi.org/10.1016/0166-218x(84)90075-1.
Colbourn, Charles, et al. Triple Systems (Oxford Mathematical Monographs). 1st ed., Clarendon Press, 1999.
Colbourn, Charles J. and Dinitz, Jeffrey H. Handbook of Combinatorial Designs, 2nd ed., CRC Press, November 2006.
Moura, Lucia. “Steiner Triple Systems.”, uOttawa, Summer 2022, https://www.site.uottawa.ca/~lucia/courses/7160-17/slides/04SteinerTripleSystems.pdf.
Weisstein, Eric W. “Steiner Triple System.” From MathWorld–A Wolfram Web Resource. https://mathworld.wolfram.com/SteinerTripleSystem.html